Towards Machine Learning Systems Design

Neil D. Lawrence

Towards Machine Learning Systems Design

2018-05-02

Neil D. Lawrence

Amazon Research Cambridge and University of Sheffield

@lawrennd inverseprobability.com

What is Machine Learning?

\[ \text{data} + \text{model} \rightarrow \text{prediction}\]

  • \(\text{data}\) : observations, could be actively or passively acquired (meta-data).
  • \(\text{model}\) : assumptions, based on previous experience (other data! transfer learning etc), or beliefs about the regularities of the universe. Inductive bias.
  • \(\text{prediction}\) : an action to be taken or a categorization or a quality score.

What is Machine Learning?

\[\text{data} + \text{model} \rightarrow \text{prediction}\]

  • To combine data with a model need:
  • a prediction function \({f}(\cdot)\) includes our beliefs about the regularities of the universe
  • an objective function \({E}(\cdot)\) defines the cost of misprediction.

Machine Learning as the Driver ...

... of two different domains

  1. Data Science: arises from the fact that we now capture data by happenstance.

  2. Artificial Intelligence: emulation of human behaviour.

What does Machine Learning do?

  • ML Automates through Data
    • Strongly related to statistics.
    • Field underpins revolution in data science and AI
  • With AI: logic, robotics, computer vision, speech
  • With Data Science: databases, data mining, statistics, visualization

"Embodiment Factors"

compute ~10 gigaflops ~ 1000 teraflops?
communicate ~1 gigbit/s ~ 100 bit/s
(compute/communicate) 10 ~ 1013

See "Living Together: Mind and Machine Intelligence"

Evolved Relationship

Evolved Relationship

Evolved Relationship

What does Machine Learning do?

  • We scale by codifying processes and automating them.
    • Ensure components are compatible (Whitworth threads)
    • Then interconnect them as efficiently as possible.
    • cf Colt 45, Ford Model T

Codify Through Mathematical Functions

  • How does machine learning work?

  • Jumper (jersey/sweater) purchase with logistic regression

\[ \text{odds} = \frac{\text{bought}}{\text{not bought}} \]

\[ \log \text{odds} = \beta_0 + \beta_1 \text{age} + \beta_2 \text{latitude}\]

Codify Through Mathematical Functions

  • How does machine learning work?

  • Jumper (jersey/sweater) purchase with logistic regression

\[ p(\text{bought}) = {f}\left(\beta_0 + \beta_1 \text{age} + \beta_2 \text{latitude}\right)\]

Codify Through Mathematical Functions

  • How does machine learning work?

  • Jumper (jersey/sweater) purchase with logistic regression

\[ p(\text{bought}) = {f}\left(\boldsymbol{\beta}^\top {{\bf {x}}}\right)\]

We call \({f}(\cdot)\) the prediction function

Fit to Data

  • Use an objective function

\[{E}(\boldsymbol{\beta}, {\mathbf{Y}}, {{\bf X}})\]

  • E.g. least squares

\[{E}(\boldsymbol{\beta}) = \sum_{i=1}^{n}\left({y}_i - {f}({{\bf {x}}}_i)\right)^2\]

Two Components

  • Prediction function, \({f}(\cdot)\)

  • Objective function, \({E}(\cdot)\)

Deep Learning

  • These are interpretable models: vital for disease etc.

  • Modern machine learning methods are less interpretable

  • Example: face recognition

Outline of the DeepFace architecture. A front-end of a single convolution-pooling-convolution filtering on the rectified input, followed by three locally-connected layers and two fully-connected layers. Color illustrates feature maps produced at each layer. The net includes more than 120 million parameters, where more than 95% come from the local and fully connected.

Source: DeepFace

Olympic Marathon Data

  • Gold medal times for Olympic Marathon since 1896.

  • Marathons before 1924 didn’t have a standardised distance.

  • Present results using pace per km.

  • In 1904 Marathon was badly organised leading to very slow times.
 image Image from Wikimedia Commons http://bit.ly/16kMKHQ

Olympic Marathon Data

Olympic Marathon Data GP

Deep GP Fit

  • Can a Deep Gaussian process help?

  • Deep GP is one GP feeding into another.

Olympic Marathon Data Deep GP

Olympic Marathon Data Deep GP

Olympic Marathon Data Latent 1

Olympic Marathon Data Latent 2

Olympic Marathon Pinball Plot

Artificial Intelligence

  • Challenges in deploying AI.

  • Currently this is in the form of "machine learning systems"

Internet of People

  • Fog computing: barrier between cloud and device blurring.
    • Computing on the Edge
  • Complex feedback between algorithm and implementation

Deploying ML in Real World: Machine Learning Systems Design

  • Major new challenge for systems designers.

  • Internet of Intelligence but currently:
    • AI systems are fragile

Fragility of AI Systems

  • They are componentwise built from ML Capabilities.
  • Each capability is independently constructed and verified.
    • Pedestrian detection
    • Road line detection
  • Important for verification purposes.

Rapid Reimplementation

  • Whole systems are being deployed.
  • But they change their environment.
  • The experience evolved adversarial behaviour.

Early AI

Machine Learning Systems Design

Adversaries

  • Stuxnet
  • Mischevious-Adversarial

Turnaround And Update

  • There is a massive need for turn around and update
  • A redeploy of the entire system.
    • This involves changing the way we design and deploy.
  • Interface between security engineering and machine learning.

Peppercorns

  • A new name for system failures which aren't bugs.
  • Difference between finding a fly in your soup vs a peppercorn in your soup.

Uncertainty Quantification

  • Deep nets are powerful approach to images, speech, language.

  • Proposal: Deep GPs may also be a great approach, but better to deploy according to natural strengths.

Uncertainty Quantification

  • Probabilistic numerics, surrogate modelling, emulation, and UQ.

  • Not a fan of AI as a term.

  • But we are faced with increasing amounts of algorithmic decision making.

ML and Decision Making

  • When trading off decisions: compute or acquire data?

  • There is a critical need for uncertainty.

Uncertainty Quantification

Uncertainty quantification (UQ) is the science of quantitative characterization and reduction of uncertainties in both computational and real world applications. It tries to determine how likely certain outcomes are if some aspects of the system are not exactly known.

  • Interaction between physical and virtual worlds of major interest for Amazon.

Example: Formula One Racing

  • Designing an F1 Car requires CFD, Wind Tunnel, Track Testing etc.

  • How to combine them?

Mountain Car Simulator

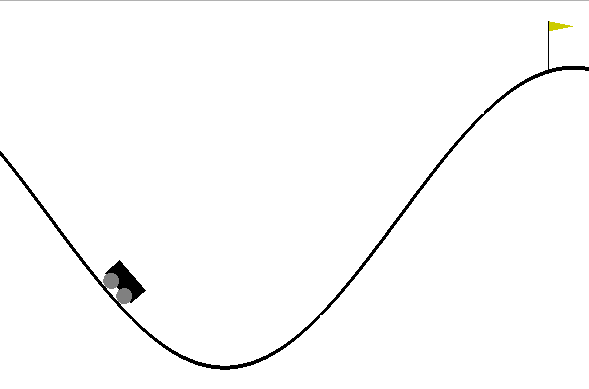
Car Dynamics

\[{{\bf {x}}}_{t+1} = {f}({{\bf {x}}}_{t},\textbf{u}_{t})\]

where \(\textbf{u}_t\) is the action force, \({{\bf {x}}}_t = (p_t, v_t)\) is the vehicle state

Policy

  • Assume policy is linear with parameters \(\boldsymbol{\theta}\)

\[\pi({{\bf {x}}},\theta)= \theta_0 + \theta_p p + \theta_vv.\]

Emulate the Mountain Car

  • Goal is find \(\theta\) such that

\[\theta^* = arg \max_{\theta} R_T(\theta).\]

  • Reward is computed as 100 for target, minus squared sum of actions

Random Linear Controller

Best Controller after 50 Iterations of Bayesian Optimization

Data Efficient Emulation

  • For standard Bayesian Optimization ignored dynamics of the car.

  • For more data efficiency, first emulate the dynamics.

  • Then do Bayesian optimization of the emulator.

  • Use a Gaussian process to model \[\Delta v_{t+1} = v_{t+1} - v_{t}\] and \[\Delta x_{t+1} = p_{t+1} - p_{t}\]

  • Two processes, one with mean \(v_{t}\) one with mean \(p_{t}\)

Emulator Training

  • Used 500 randomly selected points to train emulators.

  • Can make proces smore efficient through experimental design.

Comparison of Emulation and Simulation

Data Efficiency

  • Our emulator used only 500 calls to the simulator.

  • Optimizing the simulator directly required 37,500 calls to the simulator.

Best Controller using Emulator of Dynamics

500 calls to the simulator vs 37,500 calls to the simulator

\[{f}_i\left({{\bf {x}}}\right) = \rho{f}_{i-1}\left({{\bf {x}}}\right) + \delta_i\left({{\bf {x}}}\right)\]

Multi-Fidelity Emulation

\[{f}_i\left({{\bf {x}}}\right) = {g}_{i}\left({f}_{i-1}\left({{\bf {x}}}\right)\right) + \delta_i\left({{\bf {x}}}\right),\]

Best Controller with Multi-Fidelity Emulator

250 observations of high fidelity simulator and 250 of the low fidelity simulator

Conclusion

  • Artificial Intelligence and Data Science are fundamentally different.

  • In one you are dealing with data collected by happenstance.

  • In the other you are trying to build systems in the real world, often by actively collecting data.

  • Our approaches to systems design are building powerful machines that will be deployed in evolving environments.

Thanks!