Introduction to Machine Intelligence

SUPERINTELLIGENCE

Given for one instant an intelligence which could comprehend all the forces by which nature is animated and the respective situation of the beings who compose it—an intelligence sufficiently vast to submit these data to analysis—it would embrace in the same formulate the movements of the greatest bodies of the universe and those of the lightest atom; for it, nothing would be uncertain and the future, as the past, would be present in its eyes.

Philosophical Essay on Probabilities Laplace (1814) pg 3

If we do discover a theory of everything … it would be the ultimate triumph of human reason-for then we would truly know the mind of God

Stephen Hawking in A Brief History of Time 1988

Life

Laplace’s Gremlin

The curve described by a simple molecule of air or vapor is regulated in a manner just as certain as the planetary orbits; the only difference between them is that which comes from our ignorance.

Probability is relative, in part to this ignorance, in part to our knowledge.

Philosophical Essay on Probabilities Laplace (1814) pg 5

INTRODUCE ENTROPY TO MEASURE IGNORANCE

A Theory of Ignorance

UNCERTAINTY

But if we conceive a being whose faculties are so sharpened that he can follow every molecule in its course, such a being, whose attributes are still as essentially finite as our own, would be able to do what is at present impossible to us. For we have seen that the molecules in a vessel full of air at uniform temperature are moving with velocities by no means uniform, though the mean velocity of any great number of them, arbitrarily selected, is almost exactly uniform. Now let us suppose that such a vessel is divided into two portions, A and B, by a division in which there is a small hole, and that a being, who can see the individual molecules, opens and closes this hole, so as to allow only the swifter molecules to pass from A to B, and the only the slower ones to pass from B to A. He will thus, without expenditure of work, raise the temperature of B and lower that of A, in contradiction to the second law of thermodynamics.

Theory of Heat (Maxwell, 1871) page 308

MEASUREMENT

Measurement and Intelligence

For instance, the temperature at which ice melts is found to be always the same under ordinary circumstances, though, as we shall see, it is slightly altered by change of pressure. The temperature of steam which issues from boiling water is also constant when the pressure is constant.

These two pheomena therefore–the melting of ice and the boiling of water–indicate in a visible manner two temperatures which we may use as points of reference, the position of which depends on the properties of water and not on the conditions of our senses.

Theory of Heat Maxwell (1871) page 3

HUMANS

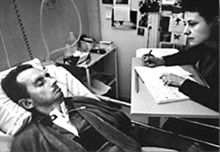
Locked In

bits/min	billions	2000	6
billion calculations/s	~100	a billion	a billion
embodiment	20 minutes	5 billion years	15 trillion years

ARTIFICIAL

Artificial Intelligence

Day by day, however, the machines are gaining ground upon us; day by day we are becoming more subservient to them; more men are daily bound down as slaves to tend them, more men are daily devoting the energies of their whole lives to the development of mechanical life. The upshot is simply PAGE 185a question of time, but that the time will come when the machines will hold the real supremacy over the world and its inhabitants is what no person of a truly philosophic mind can for a moment question.

Samuel Butler in Darwin Among the Machines a letter to the Editor of The Press, 1863

The Hamburg Hydra

ARTIFICIAL INTELLIGENCE

DeepFace

Outline of the DeepFace architecture. A front-end of a single convolution-pooling-convolution filtering on the rectified input, followed by three locally-connected layers and two fully-connected layers. Color illustrates feature maps produced at each layer. The net includes more than 120 million parameters, where more than 95% come from the local and fully connected.

Source: DeepFace (Taigman et al., 2014)

Deep Learning as Pinball

Where there be dragons

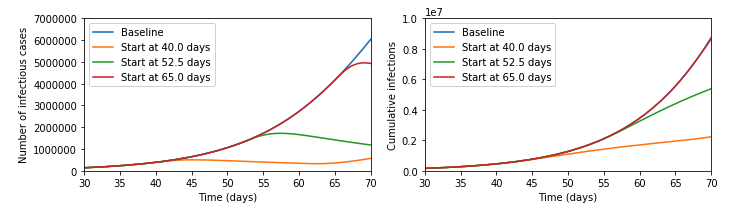
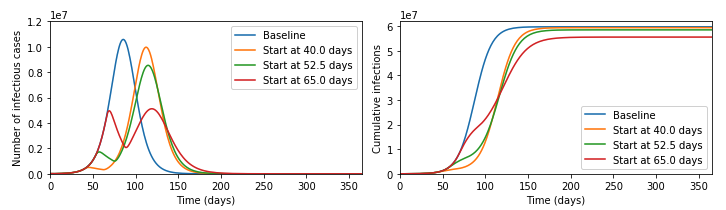
Modelling Herd Immunity

\[ \frac{\text{d}{S}}{\text{d}t} = - \beta S (I_1 + I_2). \]

\[ \frac{\text{d}{E_1}}{\text{d}t} = \beta S (I_1 + I_2) - \sigma E_1. \]

\[ \frac{\text{d}{E_2}}{\text{d}t} = \sigma E_1 - \sigma E_2. \]

\[ \frac{\text{d}{I_1}}{\text{d}t} = \sigma E_2 - \gamma I_1, \]

\[ \frac{\text{d}{I_2}}{\text{d}t} = \gamma I_1 - \gamma I_2. \]

\[ \frac{\text{d}R}{\text{d}t} = \gamma I_2. \]

Accelerate Science

• Step Change in Science through Machine Learning
• You!
• ML and the Physical World