Abstract

By contrasting our own (evolved, locked-in, embodied) intelligence with the capabilities of machine intelligence through history, The Atomic Human reveals the technical origins, capabilities and limitations of AI systems, and how they should be wielded. For engineering consultants, understanding these differences is crucial for developing effective solutions that leverage both human and machine capabilities appropriately.

Henry Ford’s Faster Horse

Figure: A 1925 Ford Model T built at Henry Ford’s Highland Park Plant in Dearborn, Michigan. This example now resides in Australia, owned by the founder of FordModelT.net. From https://commons.wikimedia.org/wiki/File:1925_Ford_Model_T_touring.jpg

It’s said that Henry Ford’s customers wanted a “a faster horse”. If Henry Ford was selling us artificial intelligence today, what would the customer call for, “a smarter human”? That’s certainly the picture of machine intelligence we find in science fiction narratives, but the reality of what we’ve developed is much more mundane.

Car engines produce prodigious power from petrol. Machine intelligences deliver decisions derived from data. In both cases the scale of consumption enables a speed of operation that is far beyond the capabilities of their natural counterparts. Unfettered energy consumption has consequences in the form of climate change. Does unbridled data consumption also have consequences for us?

If we devolve decision making to machines, we depend on those machines to accommodate our needs. If we don’t understand how those machines operate, we lose control over our destiny. Our mistake has been to see machine intelligence as a reflection of our intelligence. We cannot understand the smarter human without understanding the human. To understand the machine, we need to better understand ourselves.

The Diving Bell and the Butterfly

Figure: The Diving Bell and the Buttefly is the autobiography of Jean Dominique Bauby.

The Diving Bell and the Butterfly is the autobiography of Jean Dominique Bauby. Jean Dominique, the editor of French Elle magazine, suffered a major stroke at the age of 43 in 1995. The stroke paralyzed him and rendered him speechless. He was only able to blink his left eyelid, he became a sufferer of locked in syndrome.

See Lawrence (2024) Le Scaphandre et le papillon (The Diving Bell and the Butterfly) p. 10–12.

E S A R I N T U L
O M D P C F B V
H G J Q Z Y X K W

Figure: The ordering of the letters that Bauby used for writing his autobiography.

How could he do that? Well, first, they set up a mechanism where he could scan across letters and blink at the letter he wanted to use. In this way, he was able to write each letter.

It took him 10 months of four hours a day to write the book. Each word took two minutes to write.

Imagine doing all that thinking, but so little speaking, having all those thoughts and so little ability to communicate.

One challenge for the atomic human is that we are all in that situation. While not as extreme as for Bauby, when we compare ourselves to the machine, we all have a locked-in intelligence.

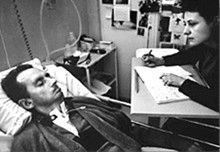
Figure: Jean Dominique Bauby was the Editor in Chief of the French Elle Magazine, he suffered a stroke that destroyed his brainstem, leaving him only capable of moving one eye. Jean Dominique became a victim of locked in syndrome.

Incredibly, Jean Dominique wrote his book after he became locked in. It took him 10 months of four hours a day to write the book. Each word took two minutes to write.

The idea behind embodiment factors is that we are all in that situation. While not as extreme as for Bauby, we all have somewhat of a locked in intelligence.

See Lawrence (2024) Bauby, Jean Dominique p. 9–11, 18, 90, 99-101, 133, 186, 212–218, 234, 240, 251–257, 318, 368–369.

Embodiment Factors

bits/min	billions	2,000
billion calculations/s	~100	a billion
embodiment	20 minutes	5 billion years

Figure: Embodiment factors are the ratio between our ability to compute and our ability to communicate. Relative to the machine we are also locked in. In the table we represent embodiment as the length of time it would take to communicate one second’s worth of computation. For computers it is a matter of minutes, but for a human, it is a matter of thousands of millions of years. See also “Living Together: Mind and Machine Intelligence” Lawrence (2017)

There is a fundamental limit placed on our intelligence based on our ability to communicate. Claude Shannon founded the field of information theory. The clever part of this theory is it allows us to separate our measurement of information from what the information pertains to.¹

Shannon measured information in bits. One bit of information is the amount of information I pass to you when I give you the result of a coin toss. Shannon was also interested in the amount of information in the English language. He estimated that on average a word in the English language contains 12 bits of information.

Given typical speaking rates, that gives us an estimate of our ability to communicate of around 100 bits per second (Reed and Durlach, 1998). Computers on the other hand can communicate much more rapidly. Current wired network speeds are around a billion bits per second, ten million times faster.

When it comes to compute though, our best estimates indicate our computers are slower. A typical modern computer can process make around 100 billion floating-point operations per second, each floating-point operation involves a 64 bit number. So the computer is processing around 6,400 billion bits per second.

It’s difficult to get similar estimates for humans, but by some estimates the amount of compute we would require to simulate a human brain is equivalent to that in the UK’s fastest computer (Ananthanarayanan et al., 2009), the MET office machine in Exeter, which in 2018 ranked as the 11th fastest computer in the world. That machine simulates the world’s weather each morning, and then simulates the world’s climate in the afternoon. It is a 16-petaflop machine, processing around 1,000 trillion bits per second.

See Lawrence (2024) embodiment factor p. 13, 29, 35, 79, 87, 105, 197, 216-217, 249, 269, 353, 369.

Bandwidth Constrained Conversations

Figure: Conversation relies on internal models of other individuals.

Figure: Misunderstanding of context and who we are talking to leads to arguments.

Embodiment factors imply that, in our communication between humans, what is not said is, perhaps, more important than what is said. To communicate with each other we need to have a model of who each of us are.

To aid this, in society, we are required to perform roles. Whether as a parent, a teacher, an employee or a boss. Each of these roles requires that we conform to certain standards of behaviour to facilitate communication between ourselves.

Control of self is vitally important to these communications.

The high availability of data available to humans undermines human-to-human communication channels by providing new routes to undermining our control of self.

The consequences between this mismatch of power and delivery are to be seen all around us. Because, just as driving an F1 car with bicycle wheels would be a fine art, so is the process of communication between humans.

If I have a thought and I wish to communicate it, I first need to have a model of what you think. I should think before I speak. When I speak, you may react. You have a model of who I am and what I was trying to say, and why I chose to say what I said. Now we begin this dance, where we are each trying to better understand each other and what we are saying. When it works, it is beautiful, but when mis-deployed, just like a badly driven F1 car, there is a horrible crash, an argument.

New Flow of Information

Classically the field of statistics focused on mediating the relationship between the machine and the human. Our limited bandwidth of communication means we tend to over-interpret the limited information that we are given, in the extreme we assign motives and desires to inanimate objects (a process known as anthropomorphizing). Much of mathematical statistics was developed to help temper this tendency and understand when we are valid in drawing conclusions from data.

Figure: The trinity of human, data, and computer, and highlights the modern phenomenon. The communication channel between computer and data now has an extremely high bandwidth. The channel between human and computer and the channel between data and human is narrow. New direction of information flow, information is reaching us mediated by the computer. The focus on classical statistics reflected the importance of the direct communication between human and data. The modern challenges of data science emerge when that relationship is being mediated by the machine.

Data science brings new challenges. In particular, there is a very large bandwidth connection between the machine and data. This means that our relationship with data is now commonly being mediated by the machine. Whether this is in the acquisition of new data, which now happens by happenstance rather than with purpose, or the interpretation of that data where we are increasingly relying on machines to summarize what the data contains. This is leading to the emerging field of data science, which must not only deal with the same challenges that mathematical statistics faced in tempering our tendency to over interpret data but must also deal with the possibility that the machine has either inadvertently or maliciously misrepresented the underlying data.

NACA Langley

The feel of an aircraft is a repeated theme in the early years of flight. In response to perceived European advances in flight in the First World War, the US introduced the National Advisory Committee on Aeronautics. Under the committee a proving ground for aircraft was formed at Langley Field in Virginia. During the Second World War Bob Gilruth published a report on the flying qualities of aircraft that characterised how this feel could be translated into numbers.

See Lawrence (2024) Gilruth, Bob p. 190-192.

Figure: 1945 photo of the NACA test pilots, from left Mel Gough, Herb Hoover, Jack Reeder, Stefan Cavallo and Bill Gray (photo NASA, NACA LMAL 42612)

See Lawrence (2024) National Advisory Committee on Aeronautics (NACA) p. 163–168. One of Gilruth’s collaborators suggested that

Hawker Hurricane airplane. A heavily armed fighter airplane noted for its role in the Battle of Britain, the Hurricane’s flying qualities were found to be generally satisfactory. The most notable deficiencies were heavy aileron forces at high speeds and large friction in the controls.

W. Hewitt Phillips²

and

Supermarine Spitfire airplane. A high-performance fighter noted for its role in the Battle of Britain and throughout WW II, the Spitfire had desirably light elevator control forces in maneuvers and near neutral longitudinal stability. Its greatest deficiency from the combat standpoint was heavy aileron forces and sluggish roll response at high speeds.

W. Hewitt Phillips³

Gilruth went beyond the reports of feel to characterise how the plane should respond to different inputs on the control stick. In other words he quantified that feel of the plane.

Gilrtuth’s work was in the spirit of Lord Kelvin’s quote on measurement

When you can measure what you are speaking about, and express it in numbers, you know something about it, when you cannot express it in numbers, your knowledge is of a meager and unsatisfactory kind; it may be the beginning of knowledge, but you have scarely, in your thoughts advanced to the stage of science.

From Chapter 3, pg 73 of Thomson (1889)

The aim was to convert a qualitative property of aircraft into quantitative measurement, thereby allowing their improvement.

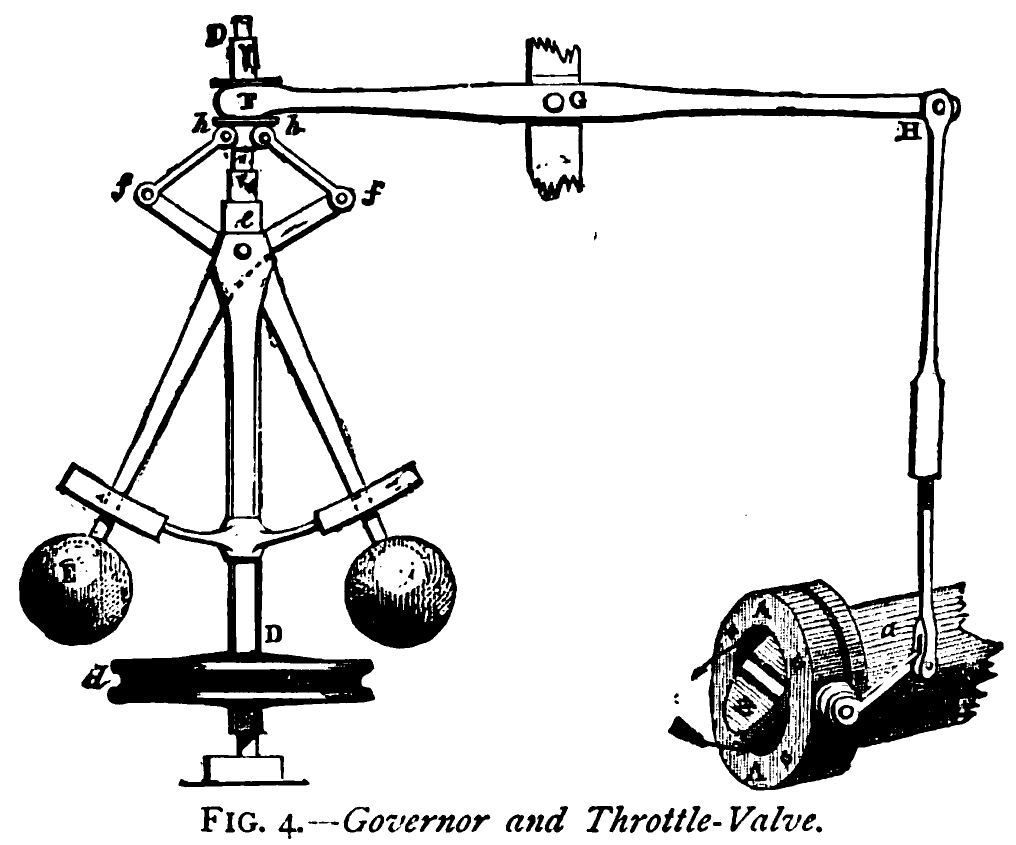
Figure: The centrifugal governor, an early example of a decision-making system. The parameters of the governor include the lengths of the linkages (which effect how far the throttle opens in response to movement in the balls), the weight of the balls (which effects inertia) and the limits of to which the balls can rise.

The evolution of feedback in engineering systems tells us a crucial story about human-machine interaction. Test pilots like Stefan Cavallo and Amelia Earhart developed an intimate understanding of their aircraft through direct physical feedback - the vibrations, the sounds, the feel of the controls. This physical connection allowed for rapid adaptation and learning.

Physical and Digital Feedback

James Watt’s governor exemplifies this physical intelligence - centrifugal force directly controlling steam flow through mechanical linkages. The feedback loop is immediate, physical, and comprehensible. Modern digital systems, however, have lost this direct connection, replacing it with layers of abstraction between sensing and action.

See Lawrence (2024) feedback loops p. 117-119, 122-130, 132-133, 140, 145, 152, 177, 180-181, 183-184, 206, 228, 231, 256-257, 263-264, 265, 329.

When Feedback Fails

The contrast between physical and digital feedback becomes stark when we examine modern system failures. While test pilots could feel their aircraft’s responses and adapt accordingly, modern digital systems often fail silently, with consequences that can go undetected for years.

The Horizon Scandal

In the UK we saw these effects play out in the Horizon scandal: the accounting system of the national postal service was computerized by Fujitsu and first installed in 1999, but neither the Post Office nor Fujitsu were able to control the system they had deployed. When it went wrong individual sub postmasters were blamed for the systems’ errors. Over the next two decades they were prosecuted and jailed leaving lives ruined in the wake of the machine’s mistakes.

Figure: The still is from the 2015 select committee.

See Lawrence (2024) Horizon scandal p. 371.

The Horizon scandal and Lorenzo NHS system represent catastrophic failures of digital feedback. Unlike a test pilot who can feel when something is wrong, or Watt’s governor which fails visibly, these digital systems created a false sense of confidence while masking their failures. The human operators - whether post office workers or healthcare professionals - were disconnected from the true state of the system, leading to devastating consequences.

The Lorenzo Scandal

The Lorenzo scandal is the National Programme for IT which was intended to allow the NHS to move towards electronic health records.

Figure: The still is from the 2011 Public Accounts committee.

The oral transcript can be found at https://publications.parliament.uk/pa/cm201012/cmselect/cmpubacc/1070/11052302.htm.

One quote from 16:54:33 in the committee discussion captures the top-down nature of the project.

Q117 Austin Mitchell: You said, Sir David, the problems came from the middle range, but surely they were implicit from the start, because this project was rushed into. The Prime Minister [Tony Blair] was very keen, the delivery unit was very keen, it was very fashionable to computerise things like this. An appendix indicating the cost would be £5 billion was missed out of the original report as published, so you have a very high estimate there in the first place. Then, Richard Granger, the Director of IT, rushed through, without consulting the professions. This was a kind of computer enthusiast’s bit, was it not? The professionals who were going to have to work it were not consulted, because consultation would have made it clear that they were going to ask more from it and expect more from it, and then contracts for £1 billion were let pretty well straightaway, in May 2003. That was very quick. Now, why were the contracts let before the professionals were consulted?

An analysis of the problems was published by Justinia (2017). Based on the paper, the key challenges faced in the UK’s National Programme for IT (NPfIT) included:

1. Lack of adequate end user engagement, particularly with frontline healthcare staff and patients. The program was imposed from the top-down without securing buy-in from stakeholders.

2. Absence of a phased change management approach. The implementation was rushed without proper planning for organizational and cultural changes.

3. Underestimating the scale and complexity of the project. The centralized, large-scale approach was overambitious and difficult to manage.

4. Poor project management, including unrealistic timetables, lack of clear leadership, and no exit strategy.

5. Insufficient attention to privacy and security concerns regarding patient data.

6. Lack of local ownership. The centralized approach meant local healthcare providers felt no ownership over the systems.

7. Communication issues, including poor communication with frontline staff about the program’s benefits.

8. Technical problems, delays in delivery, and unreliable software.

9. Failure to recognize the socio-cultural challenges were as significant as the technical ones.

10. Lack of flexibility to adapt to changing requirements over the long timescale.

11. Insufficient resources and inadequate methodologies for implementation.

12. Low morale among NHS staff responsible for implementation due to uncertainties and unrealistic timetables.

13. Conflicts between political objectives and practical implementation needs.

The paper emphasizes that while technical competence is necessary, the organizational, human, and change management factors were more critical to the program’s failure than purely technological issues. The top-down, centralized approach and lack of stakeholder engagement were particularly problematic.

Reports at the Time

Computer Weekly Report

BBC Report

Report https://publications.parliament.uk/pa/cm201012/cmselect/cmpubacc/1070/1070.pdf

This fundamental shift from physical to digital feedback represents one of the greatest challenges in modern engineering: how do we maintain meaningful human understanding and control as our systems become increasingly abstract?

See Lawrence (2024) feedback failure p. 163-168, 189-196, 211-213, 334-336, 340, 342-343, 365-366.

Figure: A Colossus Mark II codebreaking computer being operated by Dorothy Du Boisson (left) and Elsie Booker (right). Colossus was designed by Tommy Flowers, but programmed and operated by groups of Wrens based at Bletchley Park.

In the early hours of 1 June 1944, Tommy Flowers was wading ankle deep in water from a broken pipe, making the final connections to bring Mark 2 Colossus online. Colossus was the world’s first programmable, electronic, digital computer. Four days later, and Eisenhower was reading one of its first decrypts and ordering the invasion of Normandy. Flowers’s machine didn’t just launch an invasion, it launched an intellectual revolution.

See Lawrence (2024) Colossus (computer) p. 76–79, 91, 103, 108, 124, 130, 142–143, 149, 173–176, 199, 231–232, 251, 264, 267, 290, 380.

The early programmers of these systems like Dorothy and Elsie were women, but over time female programmers were marginalised from these roles Hicks (2018).

From the website of Hicks (2018).

In Programmed Inequality, Marie Hicks explores the story of labor feminization and gendered technocracy that undercut British efforts to computerize. That failure sprang from the government’s systematic neglect of its largest trained technical workforce simply because they were women. Women were a hidden engine of growth in high technology from World War II to the 1960s. As computing experienced a gender flip, becoming male-identified in the 1960s and 1970s, labor problems grew into structural ones and gender discrimination caused the nation’s largest computer user―the civil service and sprawling public sector―to make decisions that were disastrous for the British computer industry and the nation as a whole.

Blake’s Newton

William Blake’s rendering of Newton captures humans in a particular state. He is trance-like absorbed in simple geometric shapes. The feel of dreams is enhanced by the underwater location, and the nature of the focus is enhanced because he ignores the complexity of the sea life around him.

Figure: William Blake’s Newton. 1795c-1805

See Lawrence (2024) Blake, William Newton p. 121–123.

The caption in the Tate Britain reads:

Here, Blake satirises the 17th-century mathematician Isaac Newton. Portrayed as a muscular youth, Newton seems to be underwater, sitting on a rock covered with colourful coral and lichen. He crouches over a diagram, measuring it with a compass. Blake believed that Newton’s scientific approach to the world was too reductive. Here he implies Newton is so fixated on his calculations that he is blind to the world around him. This is one of only 12 large colour prints Blake made. He seems to have used an experimental hybrid of printing, drawing, and painting.

From the Tate Britain

See Lawrence (2024) Blake, William Newton p. 121–123, 258, 260, 283, 284, 301, 306.

Separation of Concerns

To construct such complex systems an approach known as “separation of concerns” has been developed. The idea is that you architect your system, which consists of a large-scale complex task, into a set of simpler tasks. Each of these tasks is separately implemented. This is known as the decomposition of the task.

This is where Jonathan Zittrain’s beautifully named term “intellectual debt” rises to the fore. Separation of concerns enables the construction of a complex system. But who is concerned with the overall system?

• Technical debt is the inability to maintain your complex software system.

• Intellectual debt is the inability to explain your software system.

It is right there in our approach to software engineering. “Separation of concerns” means no one is concerned about the overall system itself.

See Lawrence (2024) separation of concerns p. 84-85, 103, 109, 199, 284, 371.

Engineering Complexity and Understanding

The challenge of understanding complex systems has evolved dramatically since the early days of mechanical engineering. While the Apollo guidance computer contained 145,000 lines of code that were deeply understood by its creators, modern cars contain over 100 million lines. This increase in complexity isn’t just about quantity - it represents a fundamental shift in our ability to comprehend the systems we build.

The Apollo 11 landing provides a crucial lesson. When program alarms indicated computer overload, it was the deep understanding of the system’s priorities by the Mission Control team that allowed them to continue safely. This level of comprehension is increasingly rare in modern systems, where layers of abstraction and automation obscure the underlying mechanisms.

See Lawrence (2024) engineering complexity p. 198-204, 342-343, 365-366.

Intellectual Debt

Figure: Jonathan Zittrain’s term to describe the challenges of explanation that come with AI is Intellectual Debt.

In the context of machine learning and complex systems, Jonathan Zittrain has coined the term “Intellectual Debt” to describe the challenge of understanding what you’ve created. In the ML@CL group we’ve been foucssing on developing the notion of a data-oriented architecture to deal with intellectual debt (Cabrera et al., 2023).

Zittrain points out the challenge around the lack of interpretability of individual ML models as the origin of intellectual debt. In machine learning I refer to work in this area as fairness, interpretability and transparency or FIT models. To an extent I agree with Zittrain, but if we understand the context and purpose of the decision making, I believe this is readily put right by the correct monitoring and retraining regime around the model. A concept I refer to as “progression testing”. Indeed, the best teams do this at the moment, and their failure to do it feels more of a matter of technical debt rather than intellectual, because arguably it is a maintenance task rather than an explanation task. After all, we have good statistical tools for interpreting individual models and decisions when we have the context. We can linearise around the operating point, we can perform counterfactual tests on the model. We can build empirical validation sets that explore fairness or accuracy of the model.

See Lawrence (2024) intellectual debt p. 84, 85, 349, 365.

Technical Debt

In computer systems the concept of technical debt has been surfaced by authors including Sculley et al. (2015). It is an important concept, that I think is somewhat hidden from the academic community, because it is a phenomenon that occurs when a computer software system is deployed.

See Lawrence (2024) intellectual debt p. 84-85, 349, 365, 376.

Technical Consequence

Classical systems design assumes that the system is decomposable. That we can decompose the complex decision making process into distinct and independently designable parts. The composition of these parts gives us our final system.

Nicolas Negroponte, the original founder of MIT’s media lab used to write a column called ‘bits and atoms’. This referred to the ability of information to effect movement of goods in the physical world. It is this interaction where machine learning technologies have the possibility to bring most benefit.

Artificial vs Natural Systems

Let’s take a step back from artificial intelligence, and consider natural intelligence. Or even more generally, let’s consider the contrast between an artificial system and an natural system. The key difference between the two is that artificial systems are designed whereas natural systems are evolved.

Systems design is a major component of all Engineering disciplines. The details differ, but there is a single common theme: achieve your objective with the minimal use of resources to do the job. That provides efficiency. The engineering designer imagines a solution that requires the minimal set of components to achieve the result. A water pump has one route through the pump. That minimises the number of components needed. Redundancy is introduced only in safety critical systems, such as aircraft control systems. Students of biology, however, will be aware that in nature system-redundancy is everywhere. Redundancy leads to robustness. For an organism to survive in an evolving environment it must first be robust, then it can consider how to be efficient. Indeed, organisms that evolve to be too efficient at a particular task, like those that occupy a niche environment, are particularly vulnerable to extinction.

This notion is akin to the idea that only the best will survive, popularly encoded into an notion of evolution by Herbert Spencer’s quote.

Survival of the fittest

Herbet Spencer, 1864

Darwin himself never said “Survival of the Fittest” he talked about evolution by natural selection.

Non-survival of the non-fit

Evolution is better described as “non-survival of the non-fit”. You don’t have to be the fittest to survive, you just need to avoid the pitfalls of life. This is the first priority.

So it is with natural vs artificial intelligences. Any natural intelligence that was not robust to changes in its external environment would not survive, and therefore not reproduce. In contrast the artificial intelligences we produce are designed to be efficient at one specific task: control, computation, playing chess. They are fragile.

The first rule of a natural system is not be intelligent, it is “don’t be stupid”.

A mistake we make in the design of our systems is to equate fitness with the objective function, and to assume it is known and static. In practice, a real environment would have an evolving fitness function which would be unknown at any given time.

You can also read this blog post on Natural and Artificial Intelligence..

The first criterion of a natural intelligence is don’t fail, not because it has a will or intent of its own, but because if it had failed it wouldn’t have stood the test of time. It would no longer exist. In contrast, the mantra for artificial systems is to be more efficient. Our artificial systems are often given a single objective (in machine learning it is encoded in a mathematical function) and they aim to achieve that objective efficiently. These are different characteristics. Even if we wanted to incorporate don’t fail in some form, it is difficult to design for. To design for “don’t fail”, you have to consider every which way in which things can go wrong, if you miss one you fail. These cases are sometimes called corner cases. But in a real, uncontrolled environment, almost everything is a corner. It is difficult to imagine everything that can happen. This is why most of our automated systems operate in controlled environments, for example in a factory, or on a set of rails. Deploying automated systems in an uncontrolled environment requires a different approach to systems design. One that accounts for uncertainty in the environment and is robust to unforeseen circumstances.

See Lawrence (2024) natural vs artificial systems p. 102-103.

Today’s Artificial Systems

The systems we produce today only work well when their tasks are pigeonholed, bounded in their scope. To achieve robust artificial intelligences we need new approaches to both the design of the individual components, and the combination of components within our AI systems. We need to deal with uncertainty and increase robustness. Today, it is easy to make a fool of an artificial intelligent agent, technology needs to address the challenge of the uncertain environment to achieve robust intelligences.

However, even if we find technological solutions for these challenges, it may be that the essence of human intelligence remains out of reach. It may be that the most quintessential element of our intelligence is defined by limitations. Limitations that computers have never experienced.

Claude Shannon developed the idea of information theory: the mathematics of information. He defined the amount of information we gain when we learn the result of a coin toss as a “bit” of information. A typical computer can communicate with another computer with a billion bits of information per second. Equivalent to a billion coin tosses per second. So how does this compare to us? Well, we can also estimate the amount of information in the English language. Shannon estimated that the average English word contains around 12 bits of information, twelve coin tosses, this means our verbal communication rates are only around the order of tens to hundreds of bits per second. Computers communicate tens of millions of times faster than us, in relative terms we are constrained to a bit of pocket money, while computers are corporate billionaires.

Our intelligence is not an island, it interacts, it infers the goals or intent of others, it predicts our own actions and how we will respond to others. We are social animals, and together we form a communal intelligence that characterises our species. For intelligence to be communal, our ideas to be shared somehow. We need to overcome this bandwidth limitation. The ability to share and collaborate, despite such constrained ability to communicate, characterises us. We must intellectually commune with one another. We cannot communicate all of what we saw, or the details of how we are about to react. Instead, we need a shared understanding. One that allows us to infer each other’s intent through context and a common sense of humanity. This characteristic is so strong that we anthropomorphise any object with which we interact. We apply moods to our cars, our cats, our environment. We seed the weather, volcanoes, trees with intent. Our desire to communicate renders us intellectually animist.

But our limited bandwidth doesn’t constrain us in our imaginations. Our consciousness, our sense of self, allows us to play out different scenarios. To internally observe how our self interacts with others. To learn from an internal simulation of the wider world. Empathy allows us to understand others’ likely responses without having the full detail of their mental state. We can infer their perspective. Self-awareness also allows us to understand our own likely future responses, to look forward in time, play out a scenario. Our brains contain a sense of self and a sense of others. Because our communication cannot be complete it is both contextual and cultural. When driving a car in the UK a flash of the lights at a junction concedes the right of way and invites another road user to proceed, whereas in Italy, the same flash asserts the right of way and warns another road user to remain.

Our main intelligence is our social intelligence, intelligence that is dedicated to overcoming our bandwidth limitation. We are individually complex, but as a society we rely on shared behaviours and oversimplification of our selves to remain coherent.

This nugget of our intelligence seems impossible for a computer to recreate directly, because it is a consequence of our evolutionary history. The computer, on the other hand, was born into a world of data, of high bandwidth communication. It was not there through the genesis of our minds and the cognitive compromises we made are lost to time. To be a truly human intelligence you need to have shared that journey with us.

Of course, none of this prevents us emulating those aspects of human intelligence that we observe in humans. We can form those emulations based on data. But even if an artificial intelligence can emulate humans to a high degree of accuracy it is a different type of intelligence. It is not constrained in the way human intelligence is. You may ask does it matter? Well, it is certainly important to us in many domains that there’s a human pulling the strings. Even in pure commerce it matters: the narrative story behind a product is often as important as the product itself. Handmade goods attract a price premium over factory made. Or alternatively in entertainment: people pay more to go to a live concert than for streaming music over the internet. People will also pay more to go to see a play in the theatre rather than a movie in the cinema.

In many respects I object to the use of the term Artificial Intelligence. It is poorly defined and means different things to different people. But there is one way in which the term is very accurate. The term artificial is appropriate in the same way we can describe a plastic plant as an artificial plant. It is often difficult to pick out from afar whether a plant is artificial or not. A plastic plant can fulfil many of the functions of a natural plant, and plastic plants are more convenient. But they can never replace natural plants.

In the same way, our natural intelligence is an evolved thing of beauty, a consequence of our limitations. Limitations which don’t apply to artificial intelligences and can only be emulated through artificial means. Our natural intelligence, just like our natural landscapes, should be treasured and can never be fully replaced.

Engineering Consultation in the Age of AI

Engineering consultants today face a unique challenge at the intersection of human and machine capabilities. The tendency to focus purely on technical solutions can obscure crucial human factors that determine a system’s success or failure in practice.

When developing solutions, four critical factors must be balanced:

1. How will humans interact with and understand the system?
2. What assumptions are we embedding in our design?
3. How can we maintain human agency while leveraging automation?
4. Where should we prioritize explainability over efficiency?

These questions reflect the fundamental tension between human understanding and machine capability that lies at the heart of modern engineering challenges.

See Lawrence (2024) consultation challenges p. 340-341, 348-349, 351-352, 363-366, 369-370.

The MONIAC

The MONIAC was an analogue computer designed to simulate the UK economy. Analogue comptuers work through analogy, the analogy in the MONIAC is that both money and water flow. The MONIAC exploits this through a system of tanks, pipes, valves and floats that represent the flow of money through the UK economy. Water flowed from the treasury tank at the top of the model to other tanks representing government spending, such as health and education. The machine was initially designed for teaching support but was also found to be a useful economic simulator. Several were built and today you can see the original at Leeds Business School, there is also one in the London Science Museum and one in the Unisversity of Cambridge’s economics faculty.

Figure: Bill Phillips and his MONIAC (completed in 1949). The machine is an analogue computer designed to simulate the workings of the UK economy.

See Lawrence (2024) MONIAC p. 232-233, 266, 343.

Donald MacKay

Figure: Donald M. MacKay (1922-1987), a physicist who was an early member of the cybernetics community and member of the Ratio Club.

Donald MacKay was a physicist who worked on naval gun targetting during the second world war. The challenge with gun targetting for ships is that both the target and the gun platform are moving. The challenge was tackled using analogue computers, for example in the US the Mark I fire control computer which was a mechanical computer. MacKay worked on radar systems for gun laying, here the velocity and distance of the target could be assessed through radar and an mechanical electrical analogue computer.

Fire Control Systems

Naval gunnery systems deal with targeting guns while taking into account movement of ships. The Royal Navy’s Gunnery Pocket Book (The Admiralty, 1945) gives details of one system for gun laying.

Like many challenges we face today, in the second world war, fire control was handled by a hybrid system of humans and computers. This means deploying human beings for the tasks that they can manage, and machines for the tasks that are better performed by a machine. This leads to a division of labour between the machine and the human that can still be found in our modern digital ecosystems.

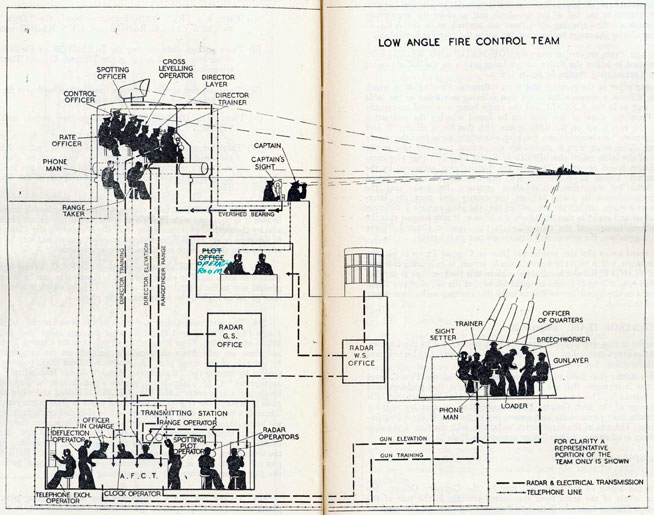
Figure: The fire control computer set at the centre of a system of observation and tracking (The Admiralty, 1945).

As analogue computers, fire control computers from the second world war would contain components that directly represented the different variables that were important in the problem to be solved, such as the inclination between two ships.

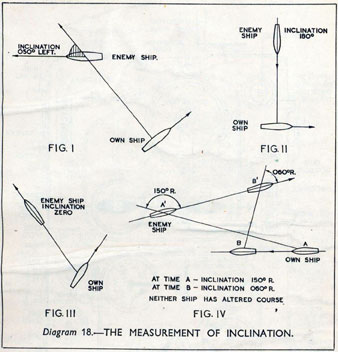
Figure: Measuring inclination between two ships (The Admiralty, 1945). Sophisticated fire control computers allowed the ship to continue to fire while under maneuvers.

The fire control systems were electro-mechanical analogue computers that represented the “state variables” of interest, such as inclination and ship speed with gears and cams within the machine.

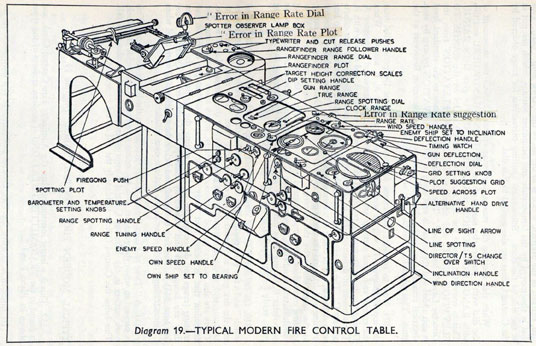
Figure: A second world war gun computer’s control table (The Admiralty, 1945).

For more details on fire control computers, you can watch a 1953 film on the the US the Mark IA fire control computer from Periscope Film.

Figure: U.S. Navy training film MN-6783a. Basic Mechanisms of Fire Control Computers. Mechanical Computer Instructional Film 27794 (1953) for the Mk 1A Fire Control Computer.

Behind the Eye

Figure: Behind the Eye (MacKay, 1991) summarises MacKay’s Gifford Lectures, where MacKay uses the operation of the eye as a window on the operation of the brain.

Donald MacKay was at King’s College for his PhD. He was just down the road from Bill Phillips at LSE who was building the MONIAC. He was part of the Ratio Club. A group of early career scientists who were interested in communication and control in animals and humans, or more specifically they were interested in computers and brains. The were part of an international movement known as cybernetics.

Donald MacKay wrote of the influence that his own work on radar had on his interest in the brain.

… during the war I had worked on the theory of automated and electronic computing and on the theory of information, all of which are highly relevant to such things as automatic pilots and automatic gun direction. I found myself grappling with problems in the design of artificial sense organs for naval gun-directors and with the principles on which electronic circuits could be used to simulate situations in the external world so as to provide goal-directed guidance for ships, aircraft, missiles and the like.

Later in the 1940’s, when I was doing my Ph.D. work, there was much talk of the brain as a computer and of the early digital computers that were just making the headlines as “electronic brains.” As an analogue computer man I felt strongly convinced that the brain, whatever it was, was not a digital computer. I didn’t think it was an analogue computer either in the conventional sense.

But this naturally rubbed under my skin the question: well, if it is not either of these, what kind of system is it? Is there any way of following through the kind of analysis that is appropriate to their artificial automata so as to understand better the kind of system the human brain is? That was the beginning of my slippery slope into brain research.

Behind the Eye pg 40. Edited version of the 1986 Gifford Lectures given by Donald M. MacKay and edited by Valerie MacKay

See Lawrence (2024) MacKay, Donald, Behind the Eye p. 268-270, 316.

Importantly, MacKay distinguishes between the analogue computer and the digital computer. As he mentions, his experience was with analogue machines. An analogue machine is literally an analogue. The radar systems that Wiener and MacKay both worked on were made up of electronic components such as resistors, capacitors, inductors and/or mechanical components such as cams and gears. Together these components could represent a physical system, such as an anti-aircraft gun and a plane. The design of the analogue computer required the engineer to simulate the real world in analogue electronics, using dualities that exist between e.g. mechanical circuits (mass, spring, damper) and electronic circuits (inductor, resistor, capacitor). The analogy between mass and a damper, between spring and a resistor and between capacitor and a damper works because the underlying mathematics is approximated with the same linear system: a second order differential equation. This mathematical analogy allowed the designer to map from the real world, through mathematics, to a virtual world where the components reflected the real world through analogy.

Human Analogue Machine

The machine learning systems we have built today that can reconstruct human text, or human classification of images, necessarily must have some aspects to them that are analagous to our understanding. As MacKay suggests the brain is neither a digital or an analogue computer, and the same can be said of the modern neural network systems that are being tagged as “artificial intelligence”.

I believe a better term for them is “human-analogue machines”, because what we have built is not a system that can make intelligent decisions from first principles (a rational approach) but one that observes how humans have made decisions through our data and reconstructs that process. Machine learning is more empiricist than rational, but now we n empirical approach that distils our evolved intelligence.

Figure: The human analogue machine creates a feature space which is analagous to that we use to reason, one way of doing this is to have a machine attempt to compress all human generated text in an auto-regressive manner.

Heider and Simmel (1944)

Figure: Fritz Heider and Marianne Simmel’s video of shapes from Heider and Simmel (1944).

Fritz Heider and Marianne Simmel’s experiments with animated shapes from 1944 (Heider and Simmel, 1944). Our interpretation of these objects as showing motives and even emotion is a combination of our desire for narrative, a need for understanding of each other, and our ability to empathize. At one level, these are crudely drawn objects, but in another way, the animator has communicated a story through simple facets such as their relative motions, their sizes and their actions. We apply our psychological representations to these faceless shapes to interpret their actions [Heider-interpersonal58].

See also a recent review paper on Human Cooperation by Henrich and Muthukrishna (2021). See Lawrence (2024) psychological representation p. 326–329, 344–345, 353, 361, 367.

The perils of developing this capability include counterfeit people, a notion that the philosopher Daniel Dennett has described in The Atlantic. This is where computers can represent themselves as human and fool people into doing things on that basis.

See Lawrence (2024) human-analogue machine p. 343–5, 346–7, 358–9, 365–8.

LLM Conversations

Figure: The focus so far has been on reducing uncertainty to a few representative values and sharing numbers with human beings. We forget that most people can be confused by basic probabilities for example the prosecutor’s fallacy.

Figure: The Inner Monologue paper suggests using LLMs for robotic planning (Huang et al., 2023).

By interacting directly with machines that have an understanding of human cultural context, it should be possible to share the nature of uncertainty in the same way humans do. See for example the paper Inner Monologue: Embodied Reasoning through Planning Huang et al. (2023).

But if we can avoid the pitfalls of counterfeit people, this also offers us an opportunity to psychologically represent (Heider, 1958) the machine in a manner where humans can communicate without special training. This in turn offers the opportunity to overcome the challenge of intellectual debt.

Despite the lack of interpretability of machine learning models, they allow us access to what the machine is doing in a way that bypasses many of the traditional techniques developed in statistics. But understanding this new route for access is a major new challenge.

HAM

The Human-Analogue Machine or HAM therefore provides a route through which we could better understand our world through improving the way we interact with machines.

Figure: The trinity of human, data, and computer, and highlights the modern phenomenon. The communication channel between computer and data now has an extremely high bandwidth. The channel between human and computer and the channel between data and human is narrow. New direction of information flow, information is reaching us mediated by the computer. The focus on classical statistics reflected the importance of the direct communication between human and data. The modern challenges of data science emerge when that relationship is being mediated by the machine.

The HAM can provide an interface between the digital computer and the human allowing humans to work closely with computers regardless of their understandin gf the more technical parts of software engineering.

Figure: The HAM now sits between us and the traditional digital computer.

Of course this route provides new routes for manipulation, new ways in which the machine can undermine our autonomy or exploit our cognitive foibles. The major challenge we face is steering between these worlds where we gain the advantage of the computer’s bandwidth without undermining our culture and individual autonomy.

See Lawrence (2024) human-analogue machine (HAMs) p. 343-347, 359-359, 365-368.

Networked Interactions

Our modern society intertwines the machine with human interactions. The key question is who has control over these interfaces between humans and machines.

Figure: Humans and computers interacting should be a major focus of our research and engineering efforts.

So the real challenge that we face for society is understanding which systemic interventions will encourage the right interactions between the humans and the machine at all of these interfaces.

Human Analogue Machine

Recent breakthroughs in generative models, particularly large language models, have enabled machines that, for the first time, can converse plausibly with other humans.

The Apollo guidance computer provided Armstrong with an analogy when he landed it on the Moon. He controlled it through a stick which provided him with an analogy. The analogy is based in the experience that Amelia Earhart had when she flew her plane. Armstrong’s control exploited his experience as a test pilot flying planes that had control columns which were directly connected to their control surfaces.

Figure: The human analogue machine is the new interface that large language models have enabled the human to present. It has the capabilities of the computer in terms of communication, but it appears to present a “human face” to the user in terms of its ability to communicate on our terms. (Image quite obviously not drawn by generative AI!)

The generative systems we have produced do not provide us with the “AI” of science fiction. Because their intelligence is based on emulating human knowledge. Through being forced to reproduce our literature and our art they have developed aspects which are analogous to the cultural proxy truths we use to describe our world.

These machines are to humans what the MONIAC was the British economy. Not a replacement, but an analogue computer that captures some aspects of humanity while providing advantages of high bandwidth of the machine.

The Atomic Human in Engineering

The connection between classical feedback control and linguistic interaction has been pioneered in the “Closed-Loop Data Science” project at the University of Glasgow led by Rod Murray-Smith (Murray-Smith et al., 2018). This EPSRC-funded research recognizes a crucial challenge: when we act on data, we change the world, potentially invalidating older data. Just as test pilots needed continuous feedback to adapt to changing conditions, modern AI systems need mechanisms for ongoing adaptation and experimentation. The project demonstrates how principles from control engineering can inform the design of interactive AI systems that maintain human agency while dealing with complex, evolving data landscapes.

The journey from Amelia Earhart’s physical intuition to modern AI interfaces reveals that human understanding comes through feedback and interaction. For engineering consultants, the challenge is to design systems that leverage the new possibilities of AI while maintaining this understanding.

The atomic human - our core intelligence that can’t be automated away - it can’t be found in raw computation or logic, but in our ability to adapt, understand, and maintain agency through feedback. Whether that feedback comes through a control stick or a conversation, the principles of good engineering - clear feedback loops, maintainable systems, and human understanding - remain essential.

See Lawrence (2024) conclusions p. 340-341, 344, 346-347, 358-359, 365-370.

Thanks!

For more information on these subjects and more you might want to check the following resources.

• book: The Atomic Human
• twitter: @lawrennd
• podcast: The Talking Machines
• newspaper: Guardian Profile Page
• blog: http://inverseprobability.com

References